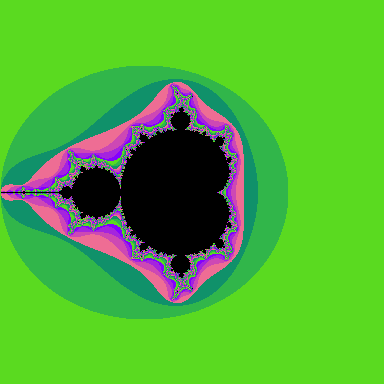
A voyage into the seldom explored Mandelbrot.

The generalized Mandelbrot set

These images correspond to the generalization of the Mandelbrot set. They refer to the exponents q=2 through q=9 (you may click on any image to enlarge):

One detail to notice is that the number of bulbs grows. In the case where q=2, there is one large bulb, while with q=3 there are two large bulbs. It is easy to see that the number of large bulbs will equal q-1.

Another interesting detail is with the butt. the number of butts increase with q and is equal to q-1. But there is always a butt on the positive x-axis, which progressively gets smaller.

What happens when q increases without bound? Let's take a look at q=13, 30, 120, 1200:

What's happening? The generalized Mandelbrot set is converging to the unit circle. (See proof ahead). And we must also recall the Mandelbrot is further tied to the circle with the appearance of the irrational number pi. This number, which represents the ratio of the diameter to the circumference of a circle, appears in different manner, as shown  by Dave Boll[D. Boll, Pi and the Mandelbrot set, http://wwwfrii.com/~dboll/mandel.html] and proved by Aaron Klebanoff [http://www.frii.com/~dboll/mandel.pdf]. This further ties the Mandelbrot set, and specifically the generalized Mandelbrot set, to an alternate definition of the concept of a circle. This is so because the circumference is not really smooth, but can be as smooth as we want it to be. This is nature's way to make circles since the circumference must eventually come down to atoms.

But what does the smooth part of the Mandelbrot "circle" (q=1200) look like on enhancement:

Let's take a closer look, sequentially zooming in on the smoothest part of the graph:

Which kind of reminds us of a gas bubbling through a liquid, complete with the bubbles bursting with a splash. Let's take two zooms at the splash:

And then zoom in for two looks at the cloudy part:

Who would ever guess that what looks like a circle is really what you observe above? Maybe only those who work in quantum chemistry and who know there are no definite borders between atoms in matter, only electron clouds.

The generalized Julia Set

Just as with the Mandelbrot set it is possible with the software to alter the exponent on the Julia iteration formula and generate interesting images. The following two correspond to a Julia set with q=5.

or the following two images for Julia sets with q=13:

The alpha generalized Mandelbrot set

The Alpha generalized Mandelbrot set also produces some very interesting images.

The following two are images of a alpha=50, q=(100,2) fractal:

Or you can also zoom into a alpha=50, q=(5000,2) fractal image, as the following four images show:

And even further with the next 3 images:

Calculation statistics.

Many of the above images can be calculated within reasonable time on a single computer running Linux or FreeBSD. But some of the images take too long. For each of the following two images, for example, which represent details of the a alpha=50, q=(2,1129) fractal, the computation time is more than twenty minutes on a pentium-IV at 1.8 Ghz, while using the PVM version of gmandel with 100 dual pentium-3 computers connected by a GByte switch,  the image generation  is cut down to only 11 seconds.

While in the future processor speeds will most certainly be able to match such performance, in the meantime the use of a computer cluster allows a peek at the fractals to be generated on  future generation desktop computers.